회사에서 성능 개선을 위해서 쓴 블로그글~~
한줄 요약하자면 백분위수를 구하기 위해서 dd-sketch 를 분석한 글이다.

논문 링크 : https://www.vldb.org/pvldb/vol12/p2195-masson.pdf
이 논문을 보고 쓴 글인데 논문 읽다가 도대체 이런건 누가 쓰는걸까 하고 저자를 찾아봤다
Jee E. Rim 이분하고 Homin K. Lee 이분 한국사람 이름인거같아서
찾아봤더니 포항공대를 나오셨다. 세상에는 참 똑똑한 사람이 많구나 저런사람들이 개발자라고 하는거지 내가 개발자라고 할 수 있을까 이런 생각이 들었다.
이런 사람들은 어떤 생각으로 살까 참 궁금하기도 하고
공부를 하면서 이 생각 저생각이 많이 들었다.
Intro. 한번은 들어본 ‘평균의 함정’
모니터링 시스템에서는 수많은 데이터가 매초 발생합니다. 이런 데이터들이 의미 없이 나열되는 것은 의미가 없습니다.
그래서 이런 데이터들을 잘 보기 위해서 자료들을 대표하는 어떤 값이 필요하게 되는데 이를 '대푯값'이라고 합니다.
대푯값은 주어진 데이터의 중심을 대표하는 값으로, 평균, 중앙값, 최빈값 등이 있습니다.

각각의 대표값들은 다양한 정보를 제공 해줍니다.
예시를 들자면 평균값은 데이터 값 들의 합을 데이터 개수로 나눈 값입니다.
평균은 자료 전체의 경향을 나타내는 값으로 이용됩니다.
하지만 특별한 이상치가 있는 경우에는 평균이 유의미한 값을 전달하기 어렵습니다.
예를 들어 95건의 데이터는 1ms이고 5건의 데이터가 1000ms 라면
평균값은 ((195) + (51000))/100 = 50ms로 유의미한 지표값을 제공해주지 못합니다.
평균값도 필요한 값이지만 다른 ‘특별한 이상치’가 있을때 볼 수 있는
지표값도 필요해 보입니다.
1. 백분위수(percentile)란?
대푯값들 중 성능 모니터링에서 빠질 수 없는 값이 있습니다. 바로 백분위수(percentile) 입니다.
백분위수는 데이터를 크기순으로 나열했을 때, 해당 위치에 있는 값을 의미합니다.
제 96 백분위수는 데이터의 96번 째 값을 의미하는 것이죠.
백분위수는 데이터의 분포를 파악하는 데 유용한 지표 중 하나입니다.
같은 예시로 95건의 데이터는 1ms이고 5건의 데이터가 1000ms 라면
95% 값을 나타낸다면 1000ms 가 될 것 입니다.
평균값인 50ms 과 차이나는것을 확인 할 수 있습니다.
특히 특정 성능 모니터링 시스템에서 이 값은 필수적 입니다.
위에 예시에서는 단순 100건이었지만 모니터링 시스템에서는
많은 요청이 대부분 정상이고 아주 소수의 데이터만 문제를 일으키는 경우가 있습니다.
이런 경우 평균에 함정에 빠지지 않고 백분위수로 데이터를 확인하는것이 효과적 입니다.
1-1. 백분위수를 구하는건 쉽지 않다
하지만 이렇게 유용한 지표인 백분위수를 구하는것은 쉽지 않은 일입니다.
백분위수를 구할때는 다음과 같은 순서로 구하게 됩니다.
- 모집단이 되는 값을 수집한다.
- 정렬한다
- 백분위수에 맞는 값을 추출한다
이렇게 3가지 단계로 계산합니다.
위 순서에서 가장 많이 시간이 걸리는 곳은 값을 정렬하는 부분입니다.
데이터가 100건이라면 금방 처리가 되겟지만
모집단이 늘어나면 늘어날수록 정렬 속도는 느려지게 됩니다.
또한 최대값이나 최소값을 구하는것은 분할계산이 가능하지만
백분위수는 분할 계산을 할 수 없습니다.
예를 들어 100개 값중에 최대값을 구한다 하면 50개 씩 나눠서 계산을 하고
최종으로 나온 두개의 값만 비교하면 됩니다.
ex> 최대값 비교시
A = {1,2,3,….49,50}
B = {501, 502,…. 550}
- A에서 나온 50, B에서 나온 550을 서로 비교.
- B에 있는 값들이 {601, 602,…. 650} 으로 바뀌면..?
- A에서 나온 50, B에서 나온 650을 비교하면 됨.
- A에서 나온 값을 다시 계산할 필요 없음.
하지만 백분위수는 50개씩 나눠서 계산을 한다고 했을때
추가로 들어오는 50개의 값에 따라
50% 값은 25가 될수도 있고, 1000이 될 수도 있습니다.
ex> 50% 값 구할시
A = {1,2,3,….49,50}
B = {501, 502,…. 550}
- A에서 나온 50%값은 25, B에서 나온 50%값은 525
- 두 집합의 50%의 평균(550/2) = 275
- 집합의 50% = 501
위에서 보는것 처럼
두 집합의 50%의 평균과 전체 집합의 50%는 서로 다르다.
분할 계산이 불가능 하다.
또한 B에 있는 값들이 {61, 62, 63, …. 110} 으로 바뀌면
A에서 나온 값을 다시 계산해야 합니다.
→ 전체 값이 다 있어야 계산을 할 수 있다.
→ 미리미리 계산을 할수가 없다
모니터링 시스템에서는 많은 양의 데이터가 실시간으로 생성됩니다.
여기서 백분위수를 구하기 위해서 모든 데이터를 저장하고 처리하는 것이 어렵고 비효율적입니다.
또한 미리 계산 할수도 없어서 해당 지표를 구하기 위해 많은 시간이 처리됩니다.
제가 소개 할 DD-Sketch는 이러한 문제를 해결하기 위해
데이터 스트림의 요약 정보를 유지하면서도 상대 오차를 컨트롤할 수 있는 방법을 제공합니다.
2. DD-Sketch는?
sketch는 큰 데이터를 처리하는데 유용한 data structure입니다.
DD-Sketch는 주어진 데이터를 일정한 크기의 버킷으로 나누고, 각 버킷에 값을 저장합니다.
값은 상대 또는 절대 오차를 사용하여 저장하고 알고리즘이 오차를 조절할 수 있습니다
데이터의 추가 및 집계 과정에서 메모리 사용량을 최적화하기 위해 동적으로 버킷의 크기를 조정합니다.
2-1. dd-sketch 기본원리
dd-sketch 에서 insert 하는 알고리즘입니다.
정확한 이해를 위해 논문에 일부를 첨부합니다.

간단 용어 설명을 하자면 다음과 같습니다.
B(버킷) : 일정한 크기로 나누어진 구간을 의미하고 특정한 값의 개수를 세는 역할
α(accurate) : 상대적 오차를 결정하는 매개변수
γ(감마) : 상대오차를 고려하여 값 범위를 조정하기 위해 사용
x를 insert 할때
- 아래 식으로 index를 구합니다

- index 를 구하기 위한 γ(감마)는 (1+α)/(1−α) 수식으로 구합니다
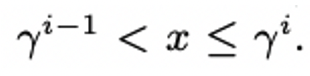
- 버킷에 해당되는 인덱스에 count +1 합니다.
한줄로 요약하자면 임의의 구간으로 나눠서 버킷이라는 곳에 count 를 저장합니다.
이렇게 버킷으로 나누게 되면 정렬을 수행하지 않고도 빠른 집계 결과를 제공합니다.
이는 대용량 데이터의 실시간 분석에 유용합니다.
또한 버킷으로 구간을 나누었기 때문에 구간이 동일한 버킷의 count 를 더하는 원리로
분할계산(mergeable)이 가능 해집니다.

sketch는 사용자의 상황에 따라서 정확도를 조절 할 수 있게끔 파라미터를 제공합니다.
이 정확도 파라미터는 메모리 사용량과 비례 합니다.
정확도가 올라가면 메모리 사용량이 올라갑니다.
다양한 Sketch 알고리즘의 특성

Sketch에는 각각 상황에 따라 선택할 수 있는 알고리즘이 있습니다.
단순 백분위수를 구하는데 어느 것이 이 특이점을 만들어 내는지 확인해 보겠습니다.
Guarantee - 보장
Sketch 알고리즘은 Rank-error(순위에러)라는 것을 사용합니다.
Rank-error(순위에러)라는 것을 사용합니다. Rank-error는 보장을 1퍼센트로 잡았을 때,
95번째의 백분위수를 구한다면 94번째에서 96번째를 보장해 줍니다.
하지만 이런 보증은 유용하지 않습니다. 왜 유용하지 않을까요?
백분위수를 보통 응답시간에 대해 많이 쓰는데 응답시간 대부분은 1초 안으로 측정이 됩니다.
하지만 문제가 되는 응답시간은 몇십초가 걸리고 몇분이 걸리는 경우도 있습니다. 그래프를 그려보면 아래처럼 파레토 분포를 따릅니다.

응답시간은 아래 처럼 짧은부분에서 대부분을 처리 하고 시간이 지날수록 처리 속도가 늘어납니다.
예시를 들어보면,
조건 : 95번째의 데이터를 가져옴. 2퍼센트의 보증율
- 93~97번째 값을 가져옴.
문제는 모니터링 시스템에서 느린 부분은 긴 꼬리처럼 파레토 분포를 따르고 있어서
93번째 ~ 97번째의 값이 드라마틱하게 달라집니다.
그래서 dd-sketch가 사용하는 Relative-error 를 사용하면 더 정확하게 값을 얻을 수 있습니다.
조건 : 95번째의 데이터를 가져옴. 2퍼센트의 보증율
- 95번째의 값이 1초라고 할때
- 0.98초 ~ 1.02초 사이를 보장
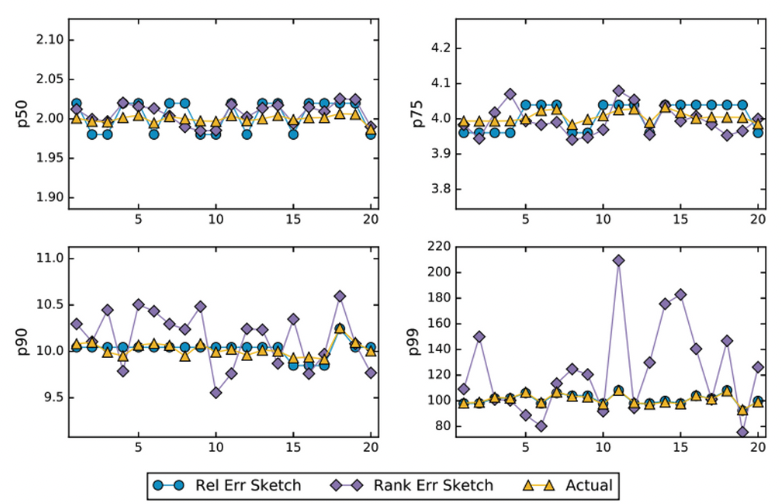
다음 그림은 Rank Error와 Relative Error의 정확성의 값을 비교한 자료입니다.
P50과 P75에서는 큰 차이를 보이지 않지만, 파레토 법칙에 따라 값이 클수록 노란색과
파란색(Relative Error Sketch)의 선이 일치하는것을 확인할 수 있습니다.
Range - 범위
DD-Sketch 와 HDR Histogram 과의 가장 큰 차이점은 Range입니다.
HDR Histogram은 Range Bounded이고 DD-Sketch는 Range Arbitrary입니다.
Range Bounded는 최솟값과 최댓값으로 제한된 범위를 가지는 것을 의미합니다.
숫자가 1부터 100 사이에 있어야 한다면, 해당 값의 범위는 1과 100 사이라는 제한이 있습니다.
100에 범위를 벗어난 값은 무시합니다.
특정 범위를 넘어서는 값들은 저장하지 않으므로 메모리 사용량을 줄이고 기록 속도를 빠르게 만들 수 있고,
이는 특정 범위에 대한 히스토그램을 작성하는 데 적합합니다.
Range Arbitrary는 데이터의 최소값과 최대값에 대한 범위를 정적으로 정의하지 않고,
데이터를 저장하는 과정에서 동적으로 범위를 조정합니다.
모니터링 시스템에서 자주 발생하는 드물게 발생하는 큰 값(특정 상황에서의 응답속도 분포)에
대해서도 처리할 수 있도록 설계되었습니다.
테스트 코드
이제 코드를 통해서 살펴보겠습니다. 해당 테스트는 라이브러리 안에 있는 테스트 코드에
테스트하기 편하게 조금 수정을 했고 사전 작업은 다음과 같습니다.

테스트 코드에서는 새로운 DD-Sketch 객체의 생성자로 indexMapping과 Store를 받습니다. 이 두 가지 인터페이스는 다양한 구현체를 가지고 있습니다.


IndexMapping의 원리
DD-Sketch 라이브러리에서는 여러 가지의 IndexMapping을 지원하는데 스케치의 상대적 정확도와 속도에 따라서 사용자는 indexMapping을 선택할 수 있습니다. indexMapping의 종류와 특징은 아래와 같으며, 이 중 제가 선택한 방법은 CubicallyInterpolatedMapping입니다.
- LogarithmicMapping을 사용하는 것이 가장 정확하나 로그를 계산하는 데 비용이 많이 들기 때문에 로그를 근사화해서 하는 방법이 효율적입니다.
- CubicallyInterpolatedMapping(삼차보간법)은 로그 매핑에 비해 메모리 오버헤드가 1%에 불과하고 로그 매핑보다 약 6배 빠르기 때문에 좋은 대안입니다. 아래 LinearlyInterpolatedMapping(선형보간법)에 비해 CubicallyInterpolatedMapping이 더 빠르고 메모리 사용성은 얼마 차이 나지 않습니다. 정확도에서 CubicallyInterpolatedMapping가 더 효율적이라 해당 구현체를 선택했습니다. 참고로 선형 보간법과 삼차 보간법은 수학적인 보간(interpolation) 기법으로, 주어진 데이터 포인트들 사이에서 누락된 값을 추정하는 데 사용됩니다.
- LinearlyInterpolatedMapping은 두 개의 인접한 데이터 포인트 사이에서 선형 방정식을 사용하여 누락된 값을 추정하는 방법입니다. 간단하고 빠르지만, 데이터 포인트 간에 선형적인 관계를 가정하기 때문에 곡선 형태의 데이터에는 정확한 결과를 얻기 어렵습니다.
- CubicallyInterpolatedMapping은 세 개의 인접한 데이터 포인트를 사용하여 누락된 값을 추정하는 방법입니다. 이 방법은 보간 함수를 이용하여 주어진 데이터 포인트들을 정확히 통과하는 곡선을 생성합니다. 삼차보간법은 더 정확한 결과를 제공할 수 있으며, 데이터 포인트 간의 곡선 관계를 더 잘 반영할 수 있습니다. 두 구현체는 선과 곡선에서 정확도 차이가 발생하게 됩니다.
IndexMapping에 다양한 구현체
다음 표는 LogarithmicMapping 매핑의 대안으로 쓸 수 있는 구현체 IndexMapping을 보여줍니다

구현체 안에서 실질적인 차이점은 아래와 같습니다.
대표적으로 LogarithmicMapping은 log를 e로 계산하지만, CubicallyInterpolatedMapping은 log를 2로 계산합니다.
또한 gamma를 구하기 위한 correctingFactor(보정계수)도 구현체마다 다릅니다.

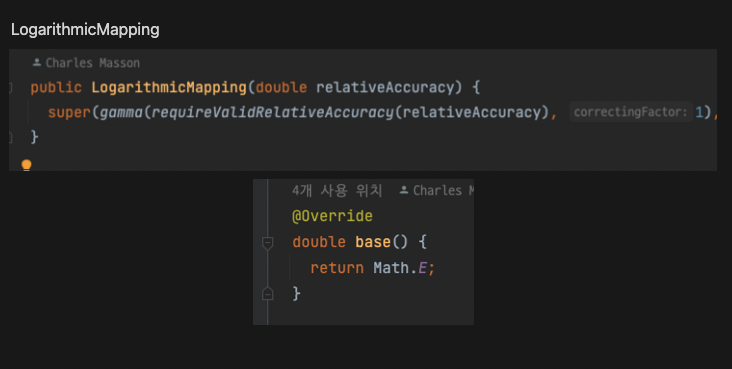
이렇게 구현체에 따라 correctingFactor, gamma 값이 다르며
사용자는 성능과 메모리에 적절한 구현체를 선택 할 수 있습니다.
3.3 dd-sketch 를 사용했을때와 비교 테스트 코드
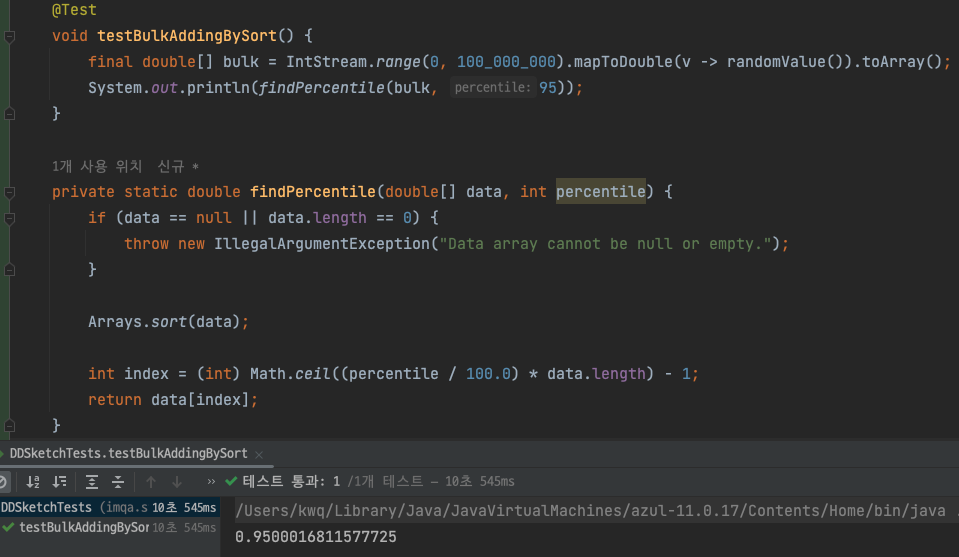
테스트는 아래와 같이 bulk insert 와 merge 가 잘 되는지 테스트 했습니다.
1억건에 모집단 데이터로 95% 값을 구하는 테스트를 진행했습니다.
dd-sketch 를 사용하지 않을때는 10초 걸리는걸 확인 할 수 있습니다.
dd-sketch 를 사용했을 했을때는 1초 가 나오는것을 확인할수 있습니다.

약 10배정도 차이나는것으로 보여집니다.
데이터 건수가 많아지면 속도 차이는 더 많이 나게 됩니다.
실제로 구한 95%의 값과, ddSketch에서 구한 95% 값의 차이를 비교해보겠습니다.

ddSketch 95% 값 = 0.9019134485492953 원본데이터의 95% 값 = 0.9500277149002122
두 값의 차이가 꽤 나는것으로 보입니다.
이것은 아까 위해서 말한 Relative-error 의 값이 0.1로 설정되어서 이런 차이가 발생했습니다.
Relative-error 값을 0.01로 설정하고 다시 테스트를 돌려보겠습니다.

수정하고 돌린 결과
ddSketch 95% 값 = 0.9526509681034269 원본데이터의 95% 값 = 0.949933244791836
값이 차이가 Relative-error 값 대로 줄어있는것을 확인 할수 있습니다.
이런 파라미터의 조절을 통해서 개발자는 95%에 해당하는 더 정확한 값을 얻을 수 있습니다.
merge 를 할때도 서로 다른 두건의 데이터가 정상적으로 merge 가 되고
p95의 대략적인 수치도 잘 나오는것을 확인 할 수 있습니다.

마무리
dd-sketch는 데이터 스트림의 요약 정보를 효과적으로 유지하면서도
정확도를 유연하게 조절할 수 있는 유용한 알고리즘입니다.
특히 백분위수를 구하는 데에 유용하며, dd-sketch를 사용하면 효율적으로 계산할 수 있습니다.
대량의 데이터를 효율적으로 처리하고 의미 있는 지표 값을 추출할 수 있습니다.
'개발' 카테고리의 다른 글
| mysql aborted clients 문제 해결 (0) | 2023.10.05 |
|---|---|
| 자바스크립트 event loop와 scope chain 이해 (1) | 2023.10.04 |
| Spring Reactive 도입기 - R2dbc에서 multiDatabaseSource (0) | 2023.07.20 |
| Azure Virtual Machines 설명 (0) | 2023.03.29 |
| Azure의 핵심 아키텍처 구성 요소 간단 정리 (0) | 2023.03.24 |


